My thesis in 5 minutes...
- The official name of my thesis is Full Waveform Inversion by Model Extension (FWIME). Like every thesis, it needs to sound smart, but the concept is quite simple.
- The goal is to improve the seismic velocity model building process when conventional methods fail due to the inaccuracy of the initial guess.
- You can find my entire thesis summarized in a series of more technical videos on my youtube channel 📺
Let me describe the 3 main novelties/contributions that my thesis brings to the table:
1. A new problem formulation
Nowadays, there exists two main families of algorithms for velocity-model building: (1) Migration velocity analysis (MVA) tends to be more robust and less sensitive to the accuracy of the initial model but produces low-resolution results, and (2) FWI (as we saw in the previous section) can recover high-resolution features of the Earth but is strongly affected by inaccurate initial guesses.
In my dissertation work, I design a new hybrid loss function formulation which merges a MVA technique with FWI into one robust and mathematically consistent workflow. By doing so, my method benefits from the robustness of MVA combined with the accuracy of FWI, while only requiring a single hyperparameter to tune.
In addition, the loss function is minimized by employing the variable projection method which helps mitigating the presence of local minima. The main novelty of my technique resides in the mathematical way I successfully pair two more conventional algorithms, which is a task that had been attempted before but with limited success.
2. An efficient industry-quality GPU implementation
Even though robust, my new loss function design increases the computational cost by at least one order of magnitude compared to more conventional methods. Therefore, I develop an industry-quality and efficient GPU numerical implementation in C++/CUDA for 3D field-data applications, which may contain tens of terabytes of data, and billions of unknown parameters to recover.
3. A 3D field data application
The last contribution is the successfuly application of my method to a deep-water node-acquisition 3D field survey acquired in the Gulf of Mexcio, which is rather rare for graduate/academic work.
Let's apply FWIME on 2 examples!
Numerical example #1: The BP 2004 model
This synthetic model, referred to as the BP 2004 model was created by industry experts as a difficult and realistic bechmark test for tomography algorithms. The model is a composite representation of velocity issues encountered in the Caspian Sea, North Sea or Trinidad (Billette and Brandsberg-Dahl, 2005).
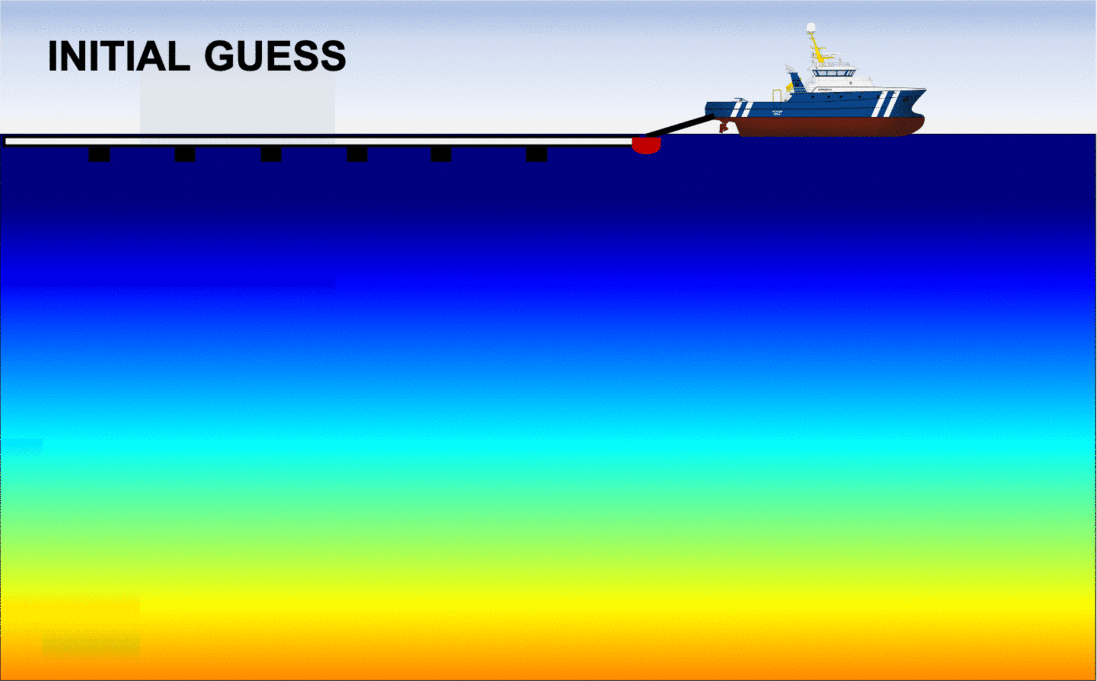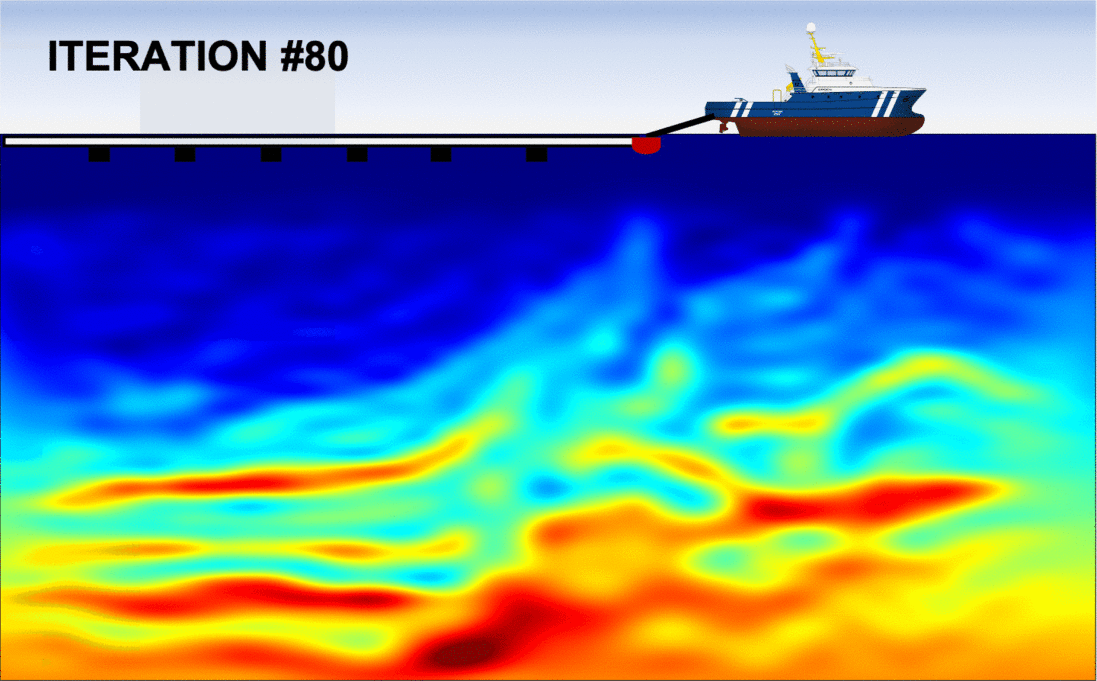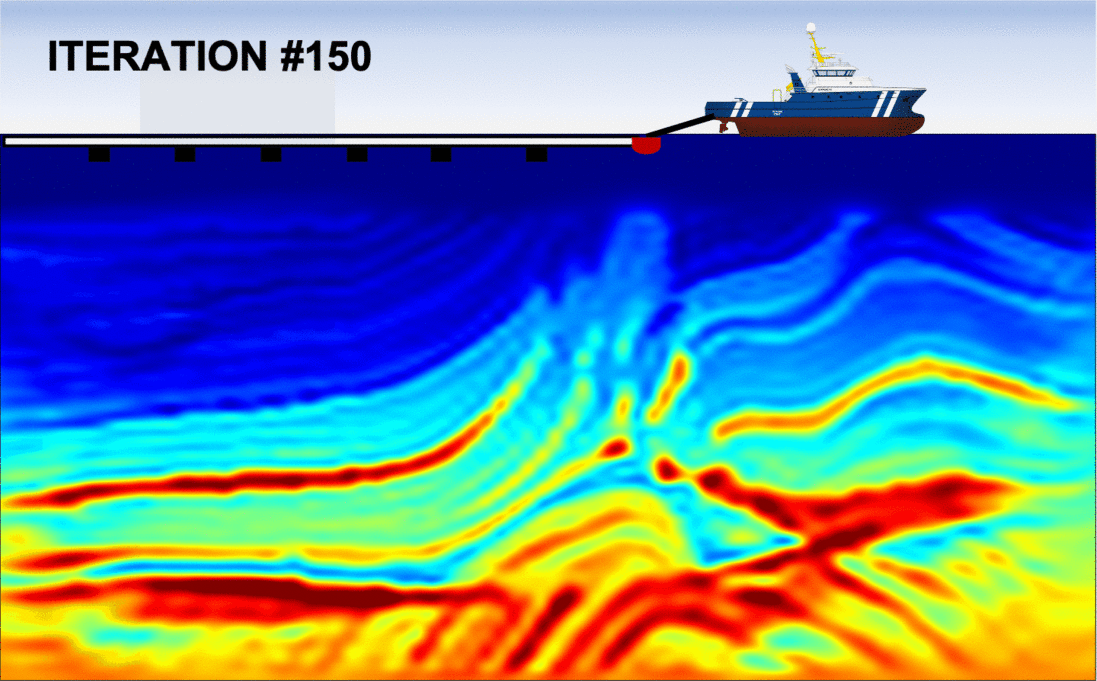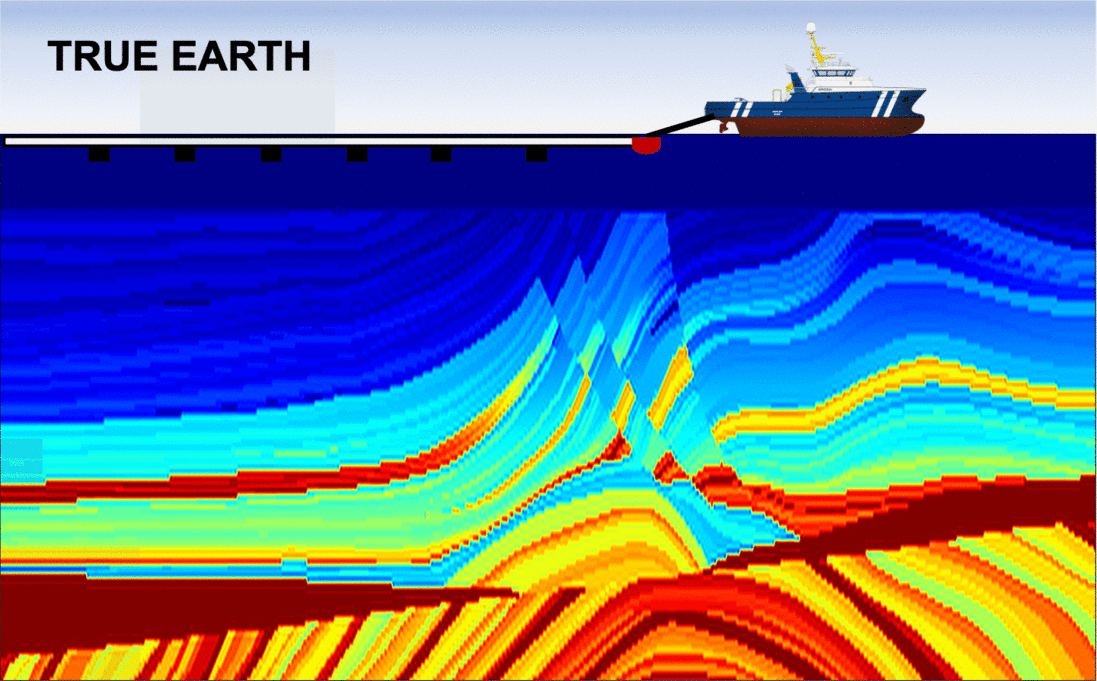
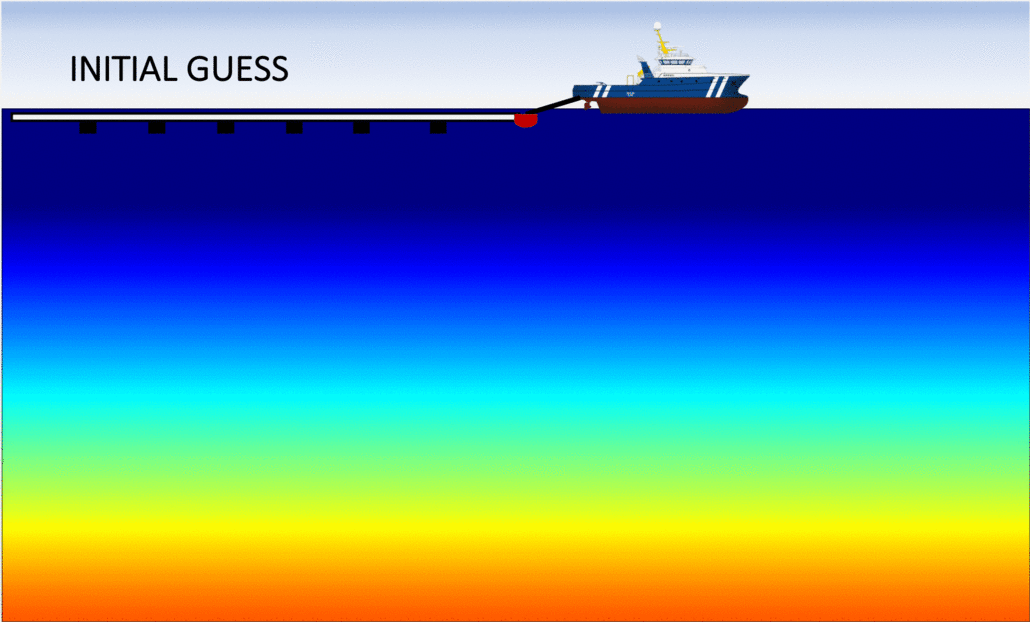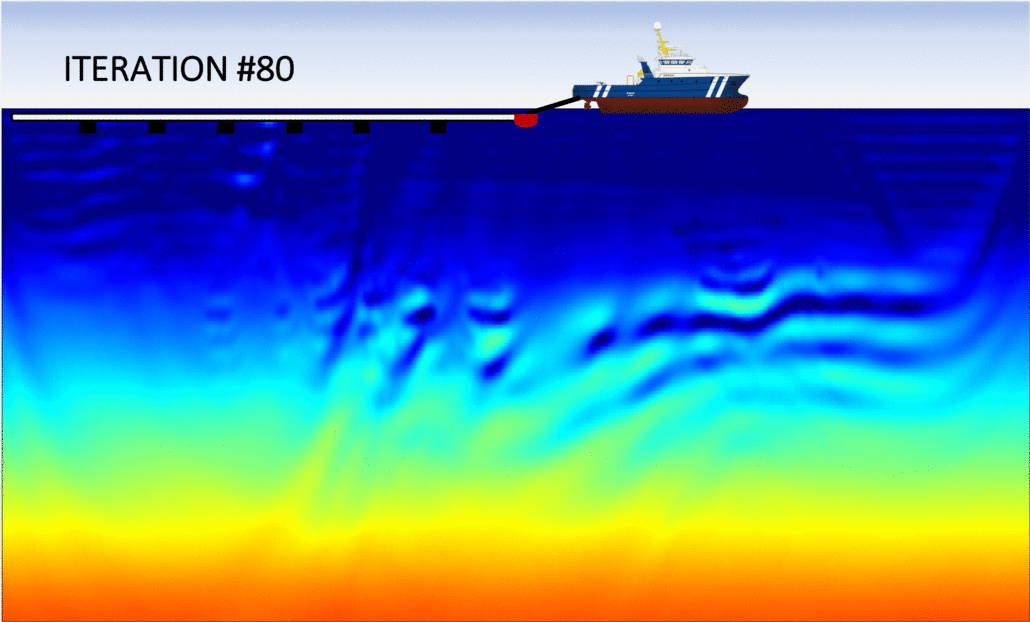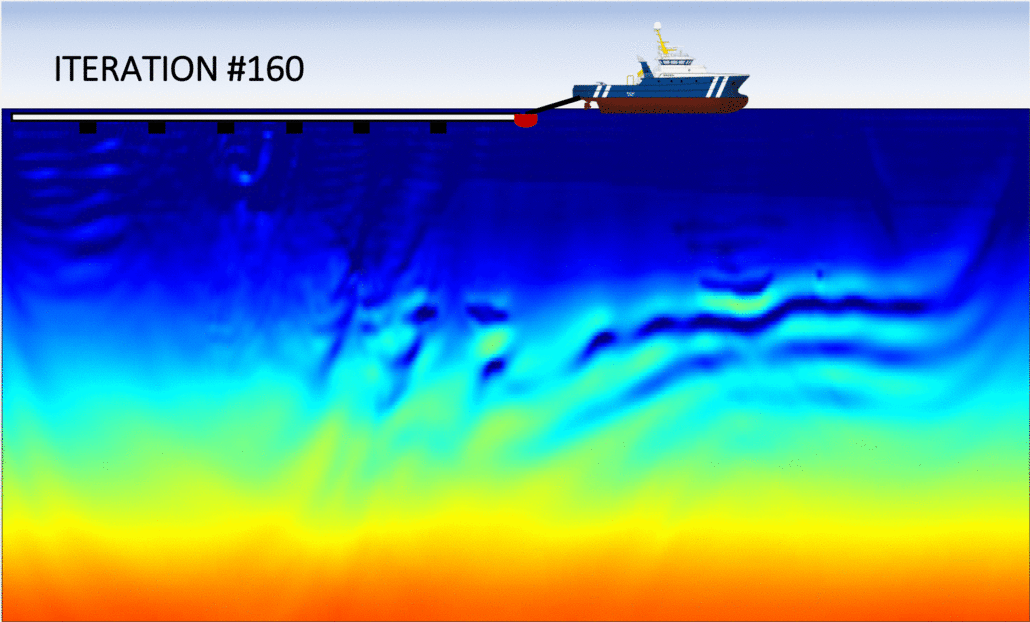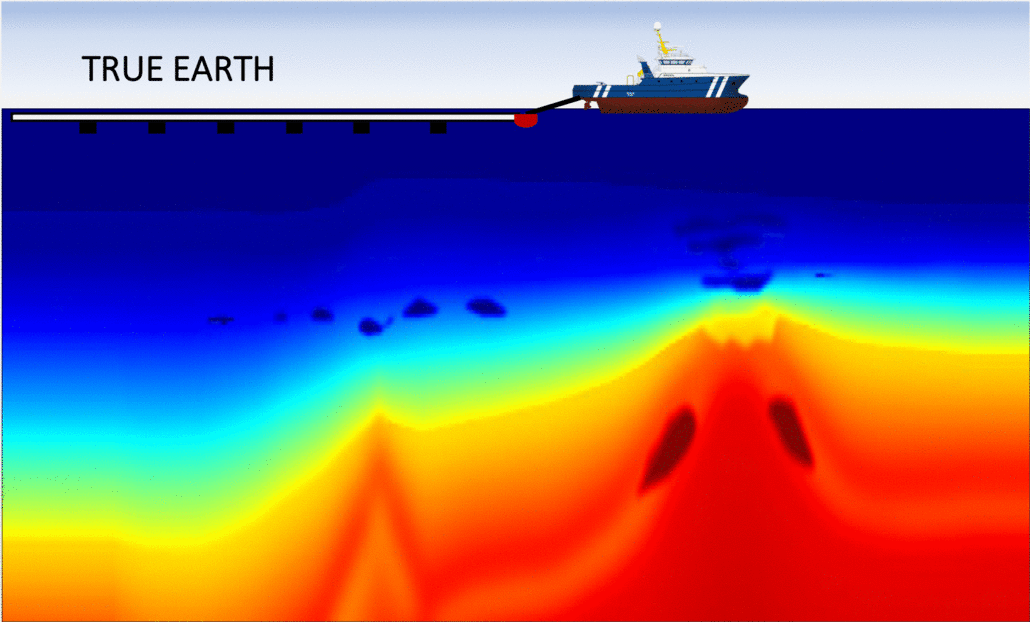
First, let us examine the left panel in the figure below, which shows the sequence of inverted models with the conventional (FWI) method. We observe that after approximately 40 iterations, the algorithm fails at updating the velocity model in a meaningful way: the optimization is "stuck" in a local minimum. As expected, this is due to the fact that the initial guess was to "far" from the true Earth, which is often the case in real applications. Consequently, the final inverted model is extremely inaccurate and will produce an unreliable migrated image.
The right panel shows the analogous sequence of inverted models, but using my algorithm (FWIME). Indeed, the same inaccurate initial model is employed. Each frame corresponds to the inverted model at a given iteration, and we can see that the algorithm manages to recover an accurate solution, almost identical to the true Earth!
Disclaimer: the figures (including the boat) are not drawn to scale! The vertical extent each panel is approximately 6 km in depth by 30 km in width.
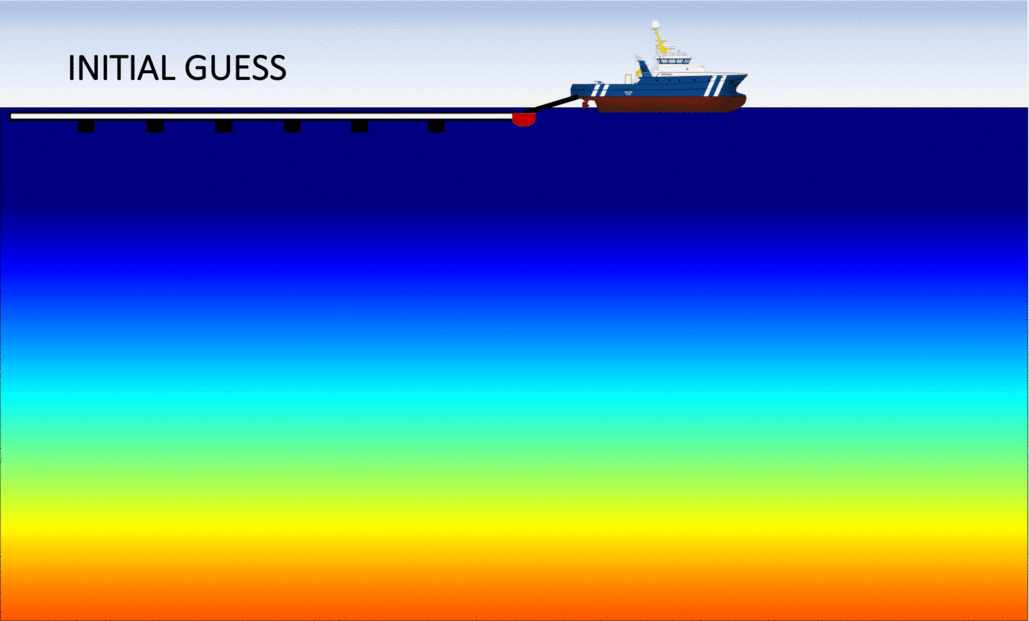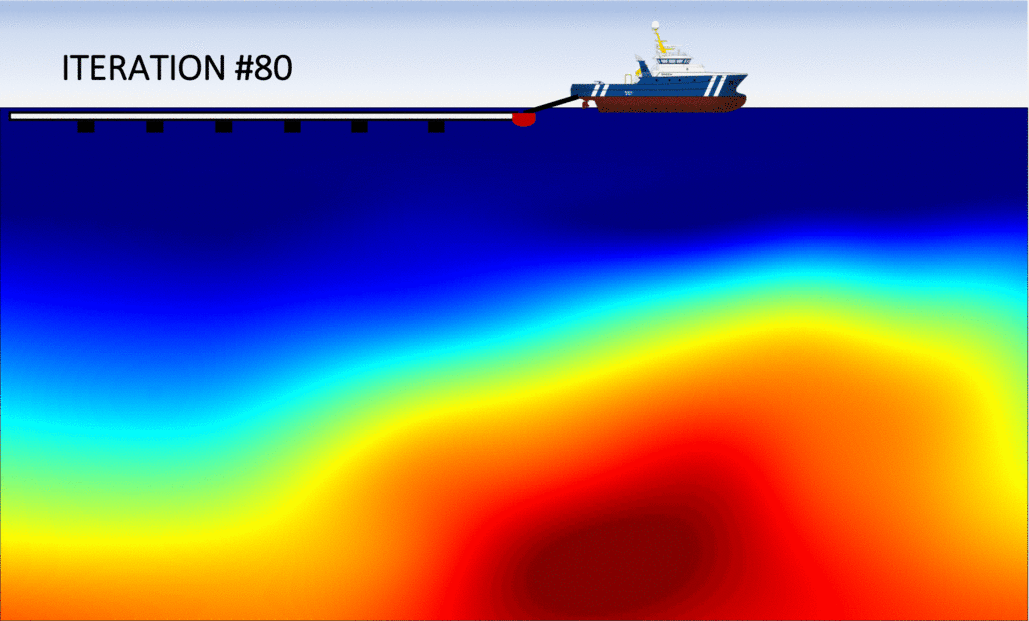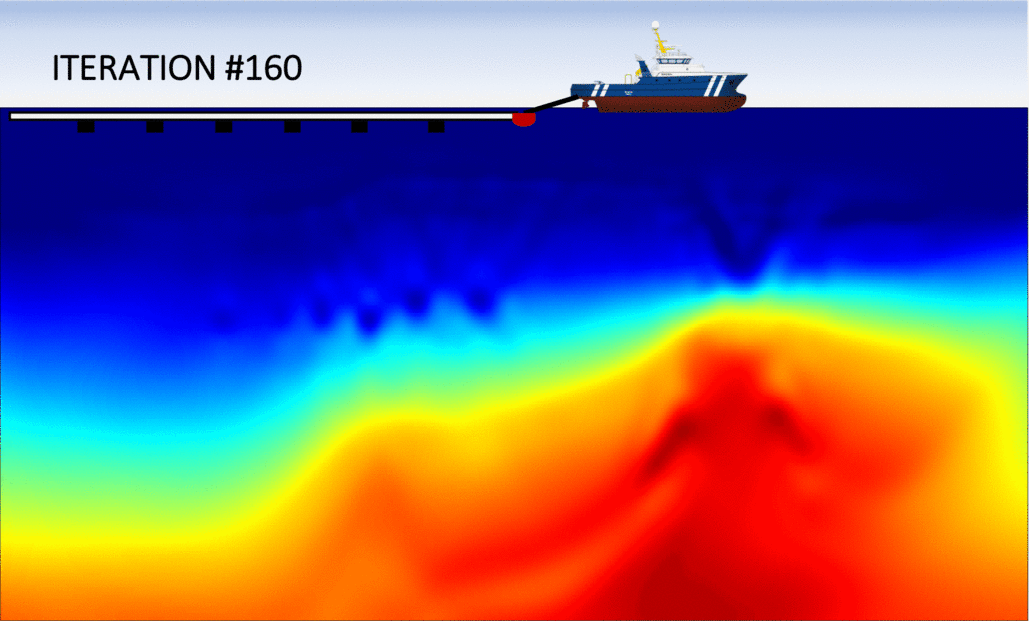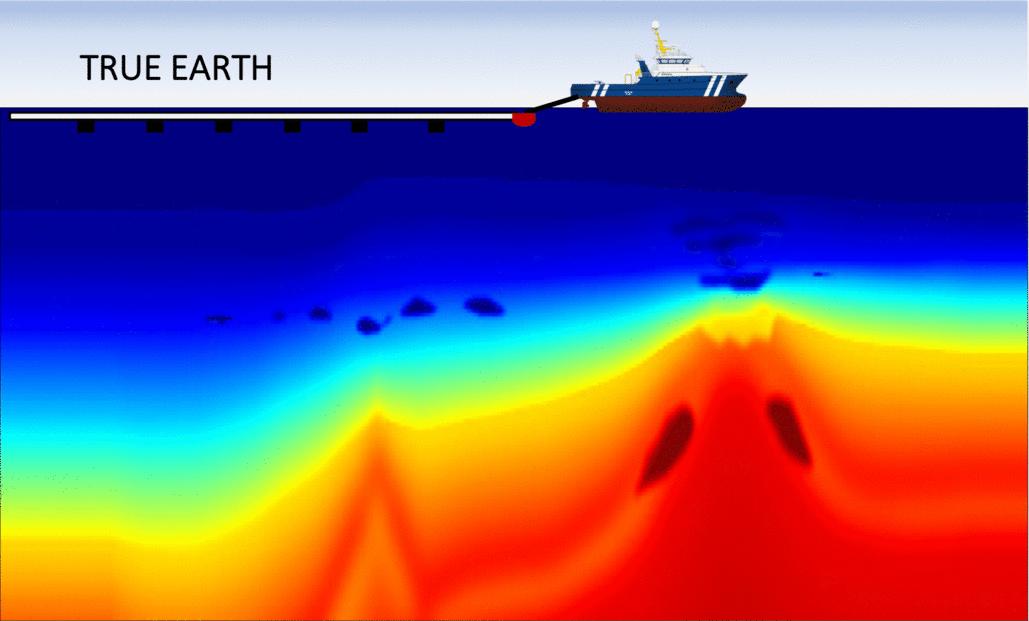
Numerical example #2: The Marmousi 2 model
The Marmousi 2 model (Martin et al., 2006) is also a well-known challenging benchmark test for velocity estimation methods. Based on a complex geological setting similar to the one found in the North Quenguela trough of the Cuanza basin (offshore Angola), it assesses the robustness of tomography algorithms. In a similar fashion as for the previous example, we begin with an uniformative initial model and show that FWIME recovers an excellent solution whereas FWI gets trapped into a local minimum.